AI中的数据表示
在第一个模块AI大世界中,我们看到了AI在各行各业发挥的重要作用。上一节中我们又学习了智能函数,这一AI领域重要的工具。那么,同学们有没有想过,我们日常生活的点点滴滴,是怎么通过智能函数与AI联系起来的呢?
在我们平时看到的很多小视频中,我们看和听到了词语、图像、视频和声音。你是否好奇过,计算机是如何理解我们说的每一个词、看到的每一幅画、播放的每一段视频和聆听的每一段声音的?通过学习本节内容,你将了解如何将复杂的信息转化为计算机可以处理的数据形式,并探索这些技术在人工智能领域的广泛应用。
1 词的表示
在计算机科学中,特别是自然语言处理领域,单词并不仅仅是我们日常所见的文字符号。为了让计算机能够理解和处理语言,我们需要将单词转化为数字形式,这就是词向量的概念。
词向量是将单词映射到一个高维空间中的数学向量,每个维度可能代表单词的某种特性或语义信息。这种表示方法使得计算机能够更好地理解词语之间的关系和语义。在图5-1这个巨大的坐标系中,每个英文单词在坐标系中都有着自己的位置。可以看到,这是一个巨大的词库组合形成的坐标系。

我们看看词向量的简单形式,也就是传统的独热码(One-Hot Encoding)。在独热码中,每个单词都被表示为一个向量,这个向量的维度等于词汇表的大小。向量中只有一个位置为1,其余位置为0。例如,如果词汇表包含"猫"、"狗"、"鸟",那么"猫"可能被表示为[1, 0, 0],"狗"表示为[0, 1, 0],"鸟"表示为[0, 0, 1]。这样,它们就能区分开来了。
那么现在我们就可以把词用向量的形式表达出来。词向量的一个重要用途是计算单词之间的相似度。如图5-2,通过比较两个词向量在向量空间中的距离,我们可以得知这两个单词在语义上的相似程度。
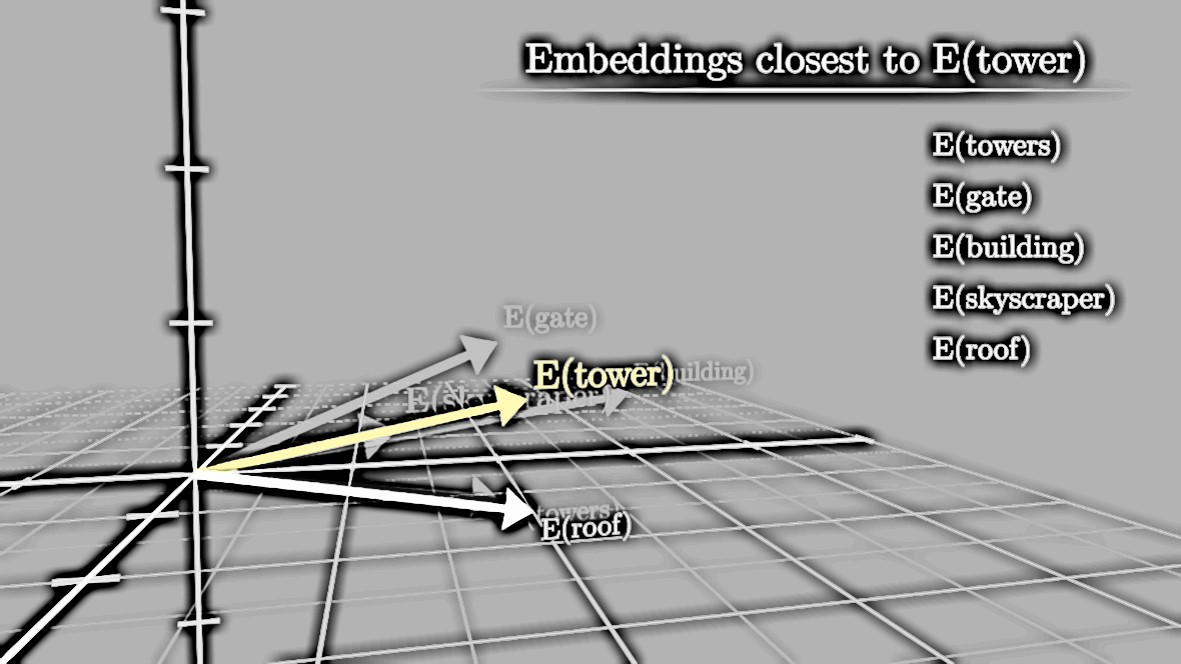
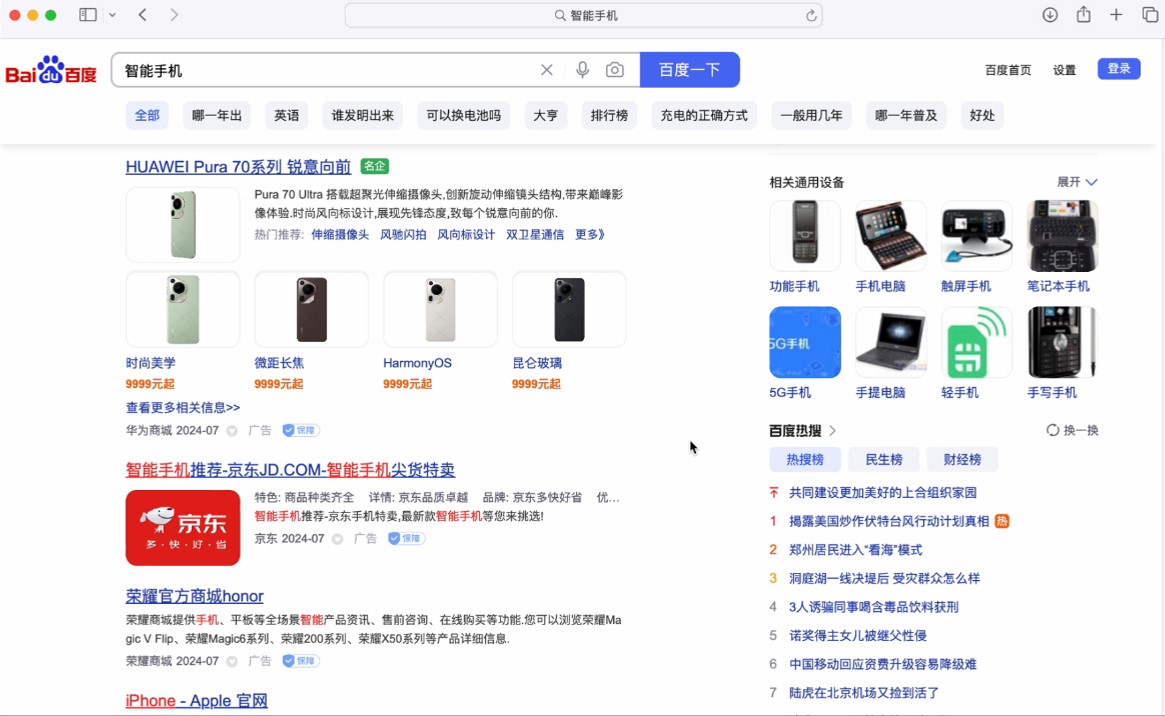
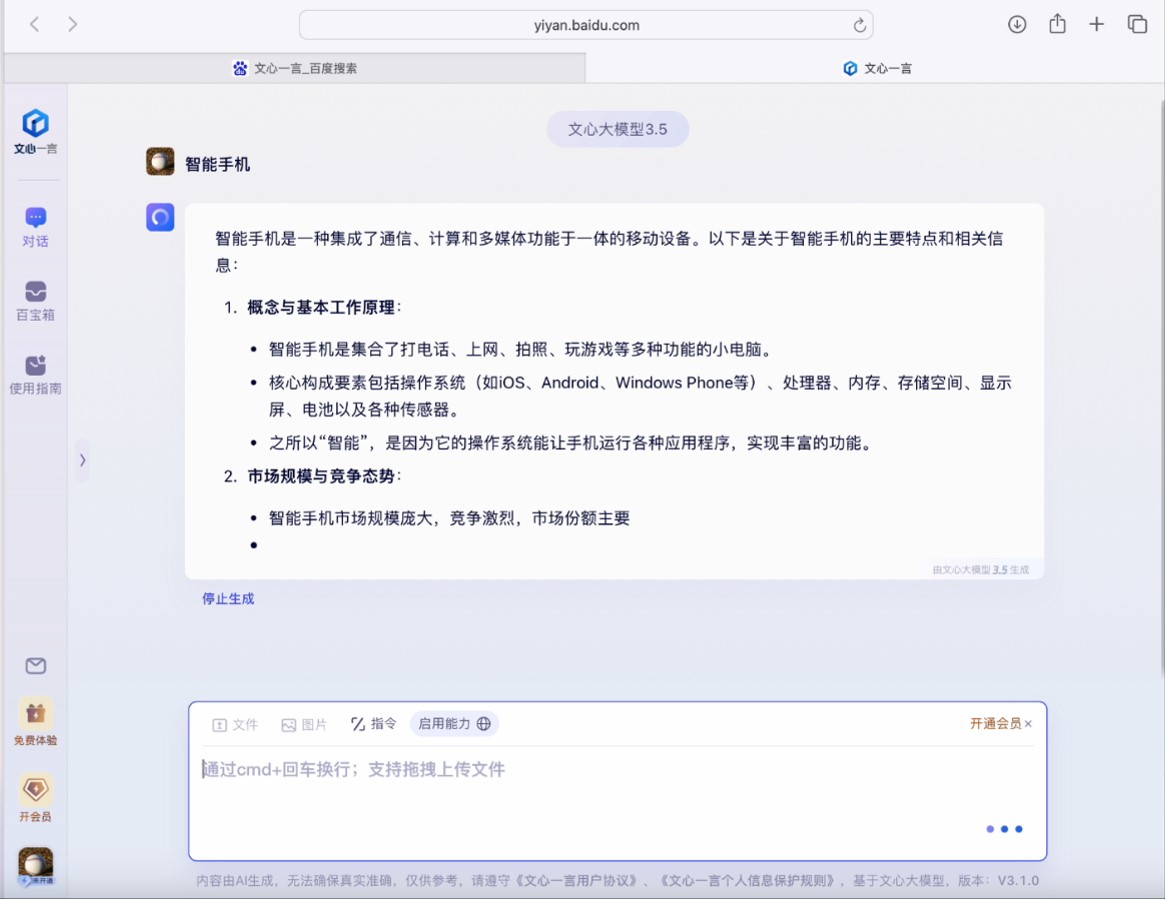
在自然语言处理任务中,词向量的应用十分广泛。如图5-3,比如在搜索引擎中,当用户输入需要查询的内容后,系统可以利用词向量来理解查询的语义,而不仅仅是匹配关键词,从而返回更加相关和精准的结果。同样,如图5-4,在智能问答系统中,词向量能够帮助计算机更好地理解用户的问题,进而提供更加准确和有用的答案。
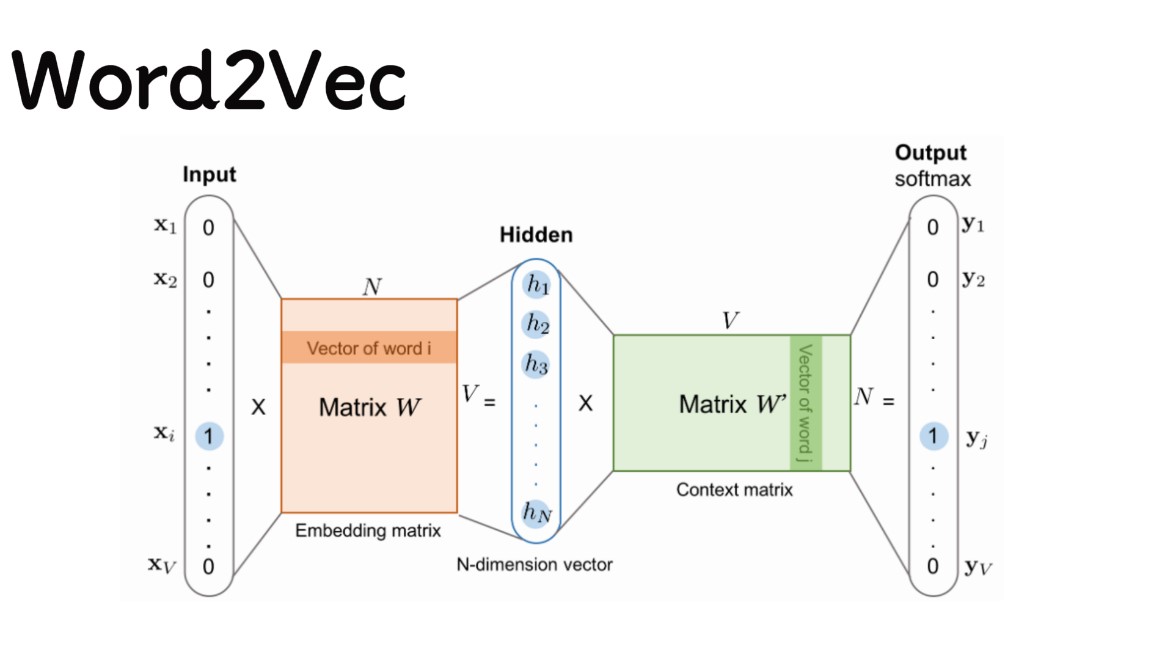
然而,独热码也有着它的缺点,最大的问题在于它不能捕捉单词之间的语义关系,同时随着词汇表的增长,向量维度也会迅速增加,导致计算效率低下。所以,相较于前面提到的独热码,更加先进的词向量表示方法如Word2Vec词向量训练模型(图5-5),能够通过分析大规模文本数据,将语义相似的单词映射到相近的向量空间位置。这种方式不仅能高效地表示单词,还能捕捉单词之间的语义关系。
让我们来看看一些有趣的例子。通过Word2Vec训练的词向量,我们可以发现“king国王”与“man男人”的向量差异和“queen女王”与“woman女人”的向量差异非常相似(图5-6)。
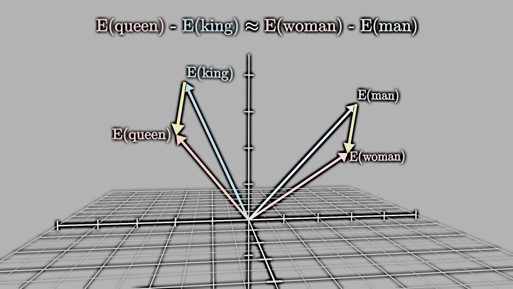
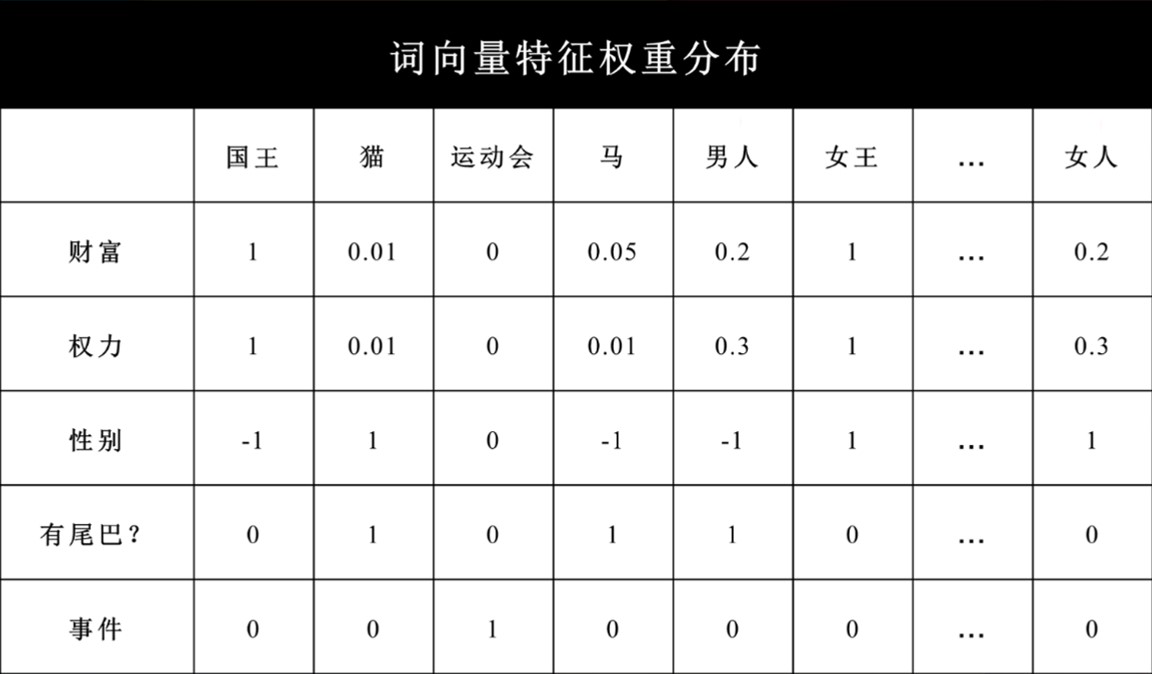
这说明Word2Vec能够理解并捕捉到单词之间的复杂语义关系,从而在向量空间中表现出这种关系。为了进一步理解词向量的表示方法,我们可以看一个词向量特征权重分布的例子(图5-7)。这里,每一列代表了不同的词语,每一行代表了某一特征上的权重。如果范围是-1到1的话,对于国王和女王来说,财富和权力都可以到1,但因为他们性别不同,在性别这个特征上一个指定为-1,一个指定为1。相比较而言,普通的男人和女人的财富和权力要小于国王和女王,所以这里定义为0.2和0.3,但在性别这个特征上与国王、女王对应,也分别指定为-1和1。
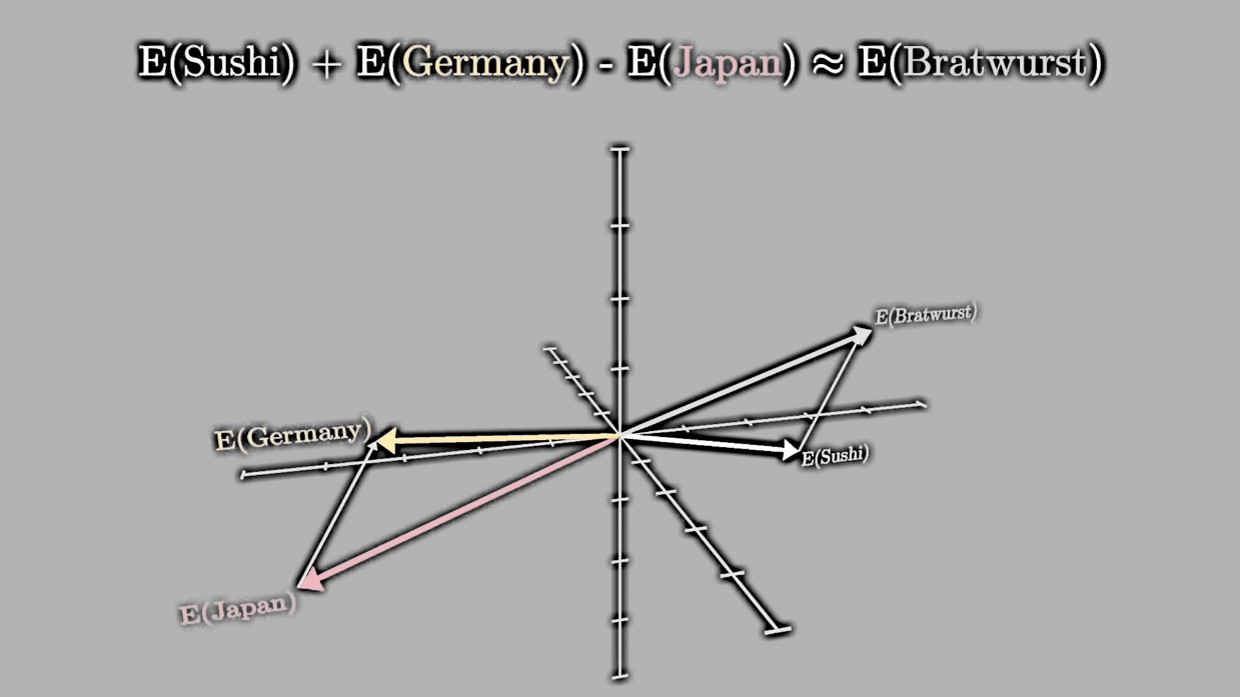
这种语义捕捉能力不仅限于性别和角色的关系,还可以扩展到其他概念。比如,“Japan日本”和“Sushi寿司”的词向量之间的关系,类似于“Germany德国”和“Bratwurst烤肠”的词向量关系(图5-8)。这种关系在向量空间中表现为相似的向量差异,体现了国家和食物的语义联系。
现在,让我们来看看这些单词是如何在词向量空间中存在的。可以看到这里每个单词都被表示为一个独特的词向量,这些向量在空间中相互关联,形成了一个复杂的语义网络。通过词向量,我们可以探索单词之间的相似性和关系,从而更深入地理解语言的奥秘。这就是词向量的魅力所在。它们为计算机理解语言提供了强大的工具,让我们能够以前所未有的方式探索语言的深层结构和意义。
2 图像的表示
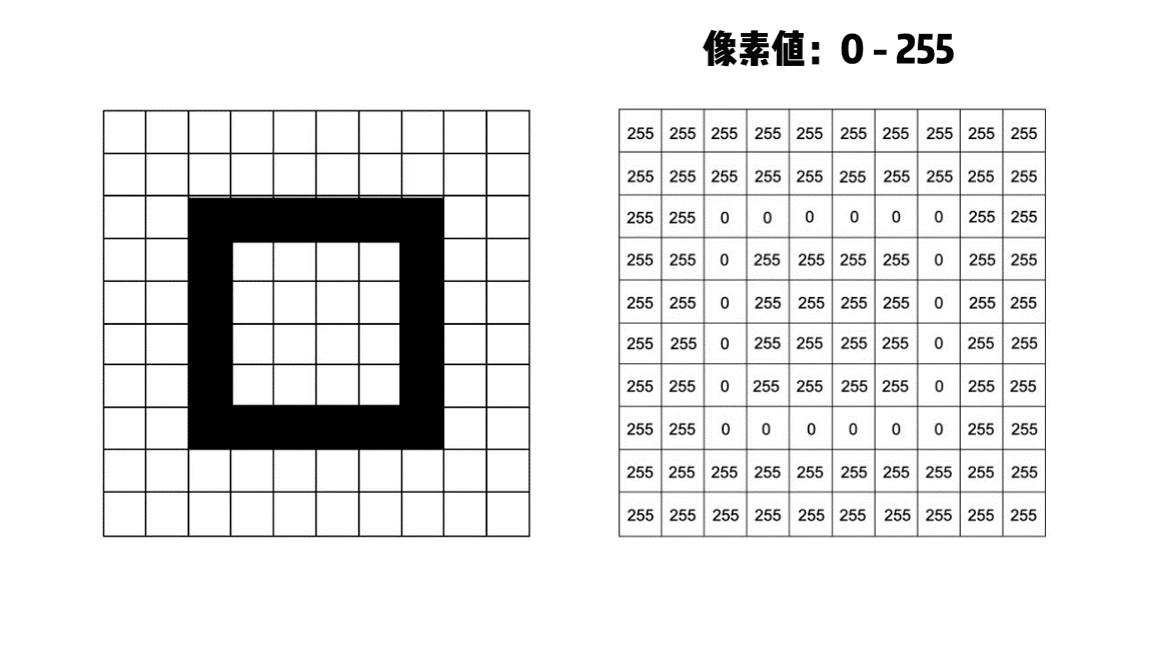
说完了词语,那么在数字世界中,图像是如何被表示的呢?简单来说,图像可以被视为一个由像素值组成的矩阵。每个像素都是图像中的一个小点,它记录了该点的灰度值信息。如图5-9,灰度值是一个介于0到255之间的数值,用来表示像素的亮度,其中0代表黑色,255代表白色,其他数值则表示不同的灰度级别。将所有这些像素按照行和列的顺序排列起来,就形成了一个像素矩阵,这就是灰度图像在计算机中的基本表示形式。

相较于灰度值图片,我们日常看到的更多是彩色图像(图5-10)。

那么彩色图像是如何表示的呢?在彩色图像中,每个像素的颜色通常由红、蓝、绿三种颜色的不同组合来表示,这就是RGB颜色模型(图5-11)。RGB模型通过调整这三种颜色的强度值来实现各种颜色的呈现。

具体来说,一张彩色图像可以用三个二维矩阵来表示,每个矩阵分别对应红色、绿色和蓝色通道。矩阵中的每个元素都代表该颜色通道在对应像素点上的强度值,数值范围通常是0到255。这样,每个像素点的颜色是由这三个强度值组合而成的。
例如,一幅1920x1080分辨率的彩色图像实际上由三个1920x1080的矩阵组成。第一个矩阵记录红色通道的强度值,第二个矩阵记录绿色通道的强度值,第三个矩阵记录蓝色通道的强度值。通过将这三个矩阵重新组合,我们就可以还原出原始的彩色图像。如图5-12,无论是风景照、人物照还是抽象艺术,它们都被表示为一组或多组二维矩阵。这些矩阵记录了图像中每个像素点的颜色信息,从而构成了我们看到的丰富多彩的世界。通过这些例子,我们可以清楚地看到,图像数据的矩阵表示方式不仅仅是一种存储方式,更是计算机处理和理解图像的基础。

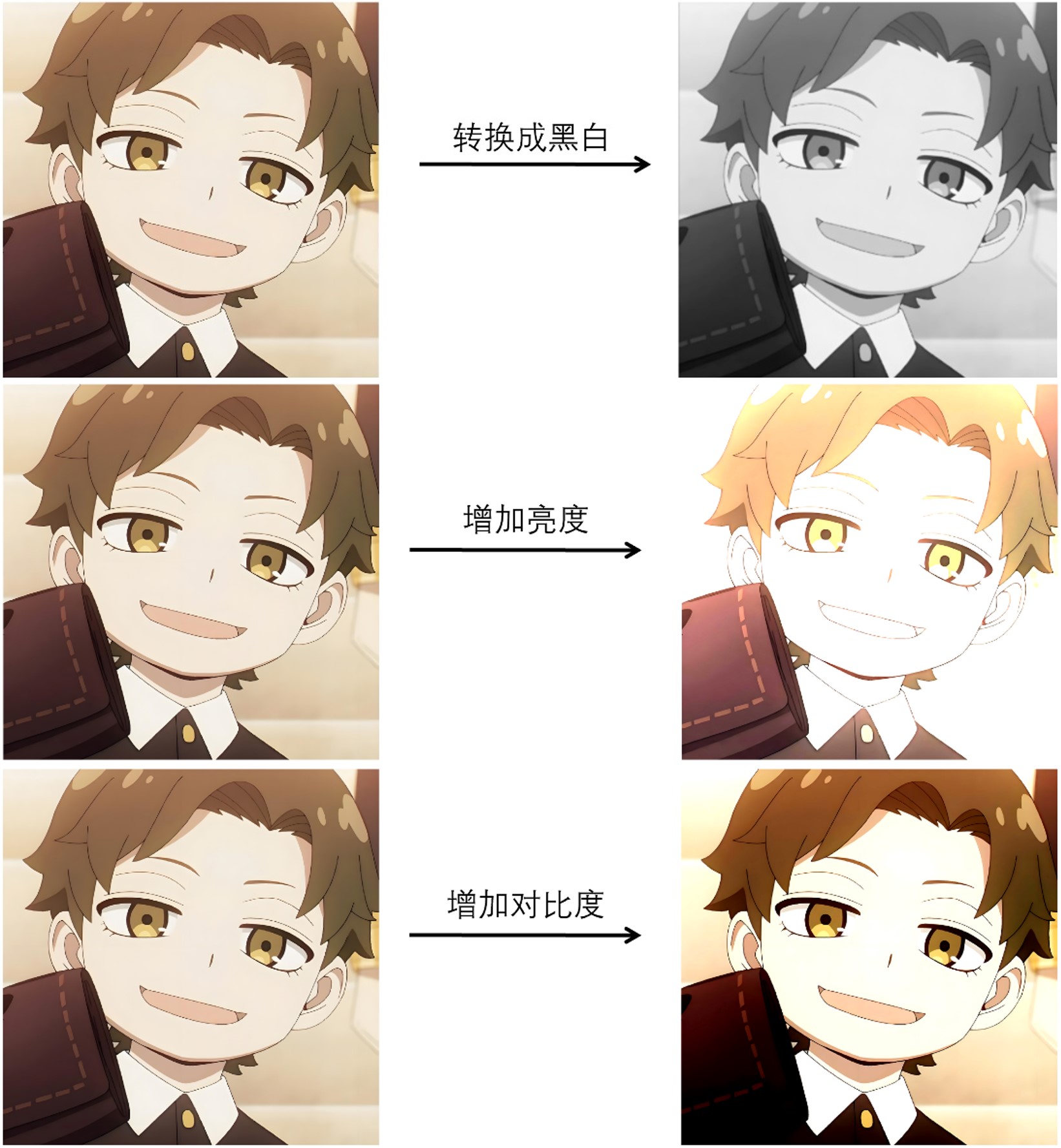
通过像素矩阵的表示方法,我们能够将图像这种直观的视觉信息转化为计算机可以处理的数字数据。这种表示方式不仅方便我们存储和传输图像数据,还为我们提供了许多分析和处理图像的强大工具。例如,通过改变像素矩阵中的值,我们可以实现各种滤镜效果,如将图像转换为黑白、增加亮度或对比度等(图5-13)。
此外,利用像素矩阵表示法 ,我们还可以进行复杂的图像处理任务。例如,通过比较不同图像的像素矩阵,我们可以进行图像识别和匹配,从而实现人脸识别、目标检测等功能。在医学领域,图像矩阵可以帮助医生分析X光片或MRI图像,辅助诊断疾病。
这种基于像素矩阵的表示方法,也为机器学习和人工智能的发展提供了基础。在训练图像分类或目标检测模型时,我们常常使用大量标注好的图像矩阵数据来教计算机识别各种物体和场景。通过这些应用,我们可以看到,图像矩阵不仅是计算机存储图像的一种方式,更是图像处理和分析的核心工具。
总的来说,像素矩阵的表示方法使得我们能够高效地存储、传输和处理图像数据,为各种图像应用提供了基础。从日常的照片编辑到前沿的人工智能研究,这种表示方法无处不在,发挥着重要的作用。
3 视频的表示
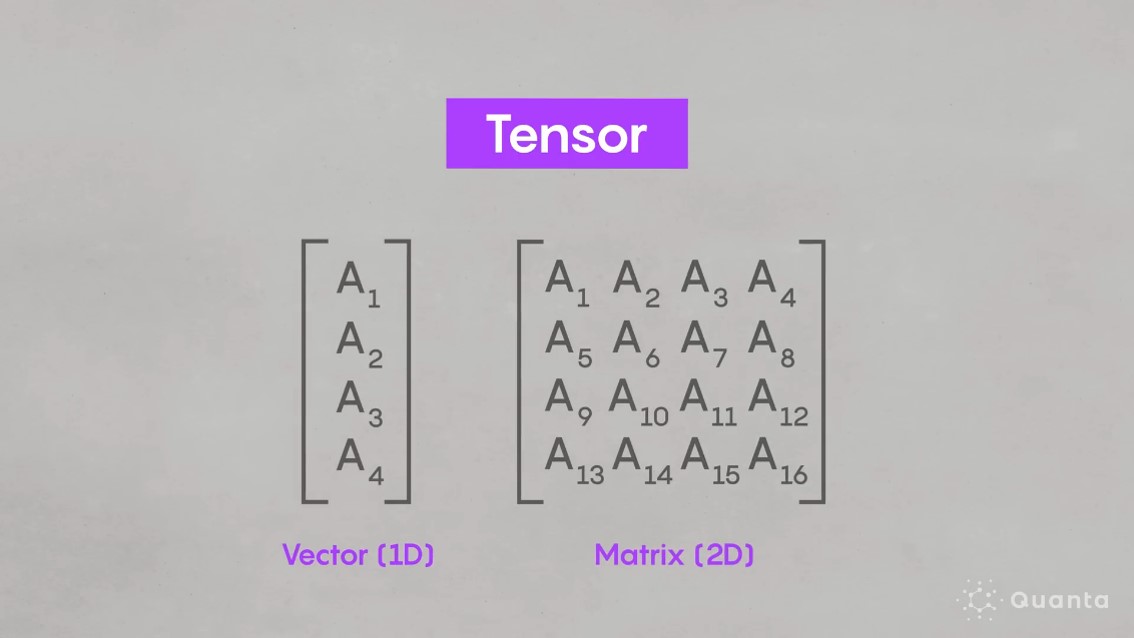
说完了图像,当我们谈论视频的表示时,实际上是在谈论一个更高维度的数据结构——张量。提到张量,或许有些同学会感到些许陌生,但想象一下童年时代,我们或许都玩过走马灯(图5-14)或是看过翻页动画(图5-15)。记得那些色彩斑斓的纸片,在快速旋转或一页页翻动之下,原本静止的画面仿佛被赋予了生命,连贯起来就构成了一段段生动有趣的视频片段。这正是视频表示的核心所在:它不仅仅是单幅图像的简单堆砌,而是将无数张图像沿着时间的轴线巧妙地串联起来,形成了一个连续、动态的数据流。每一帧图像,都像是时间轴上的一个节点,记录着那一刻的光影与色彩;而当这些节点以特定的速率被连续播放时,因为视觉暂留现象,就创造出了我们眼中那流畅、生动的视频。


图像可以视为一个三维张量,包含宽度、高度和颜色通道三个维度。而视频则是这些连续图像帧的集合,因此,它增加了一个时间维度(如图5-16),形成了一个四维张量。这种四维张量的每个元素代表了视频中特定时间点上的像素值。视频的表示不仅仅包括每帧图像的空间信息,还包括帧与帧之间的时间顺序关系。
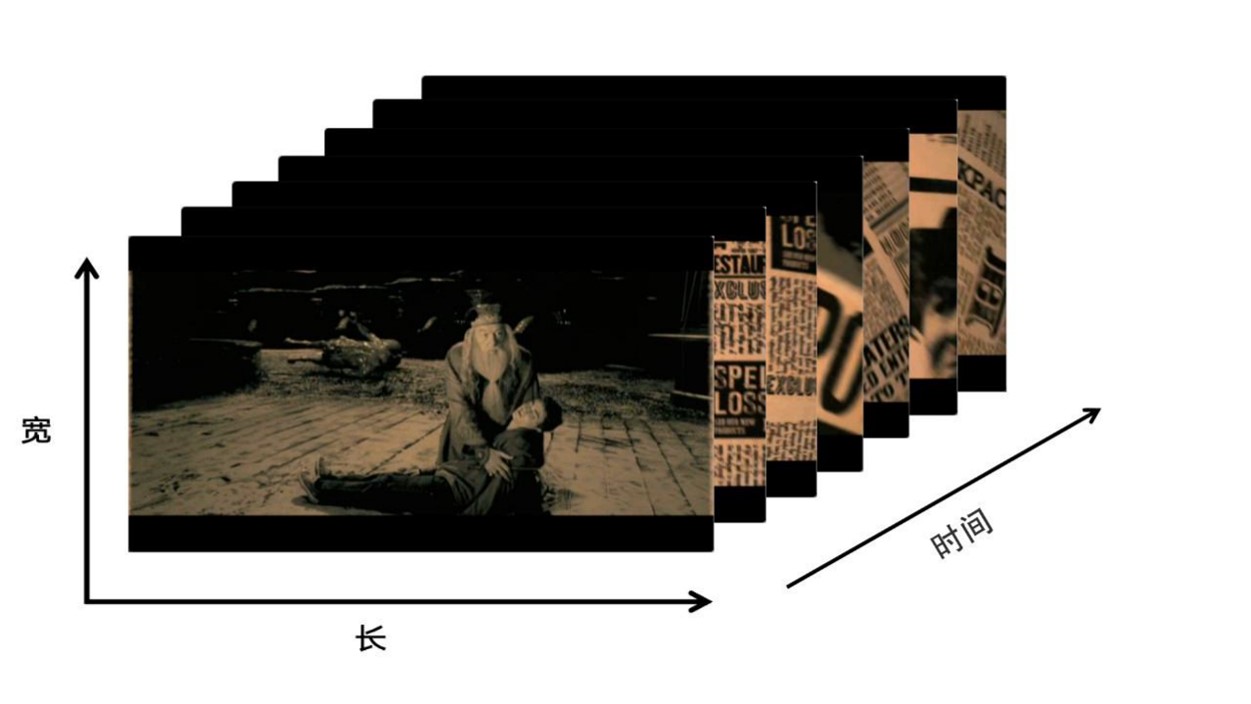
逐帧播放视频,我们可以观察到每一帧之间的差异和联系,这些差异和联系共同构成了视频的视觉内容和动态效果。通过时间维度,我们可以看到一个人的表情变化、运动员的动作、云彩的移动、动物的活动等等,这些都是通过时间维度的变化来呈现的。
通过这样的高维度张量表示方式,我们能够更深入地理解和处理视频数据。这种理解不仅限于视觉内容的感知,还包括对视频中复杂动态信息的分析和应用。例如,在视频监控中,可以通过分析视频帧的变化来检测异常行为;在虚拟现实中,可以利用视频数据来创建沉浸式体验。通过理解和处理这种高维度数据结构,我们能够更全面地探索和利用视频中蕴含的丰富信息,推动视觉技术的进步和应用的拓展。
4 声音的表示
声音作为日常生活中无处不在的媒介,实际上隐藏着丰富的信息。首先,我们来了解一下声音数据的特点。声音数据通常以波形图的形式呈现,展示声音的振幅、频率等基本信息。但要更有效地利用声音数据,我们通常需要将其转换为向量形式。
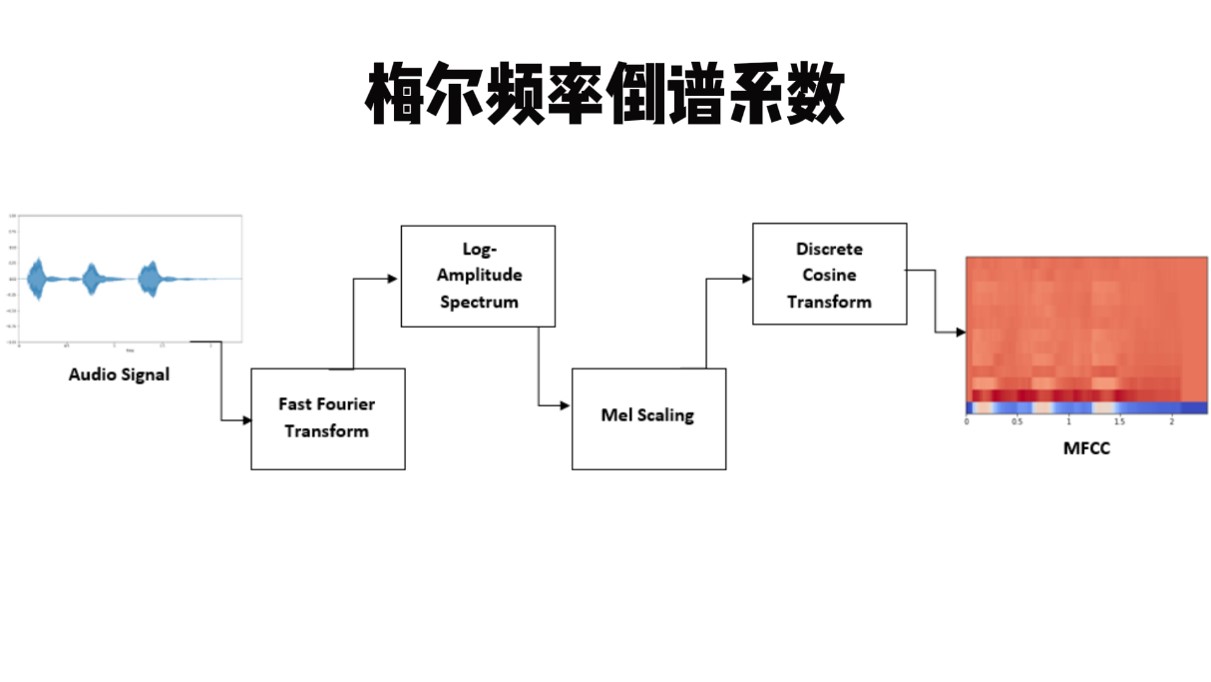
为了处理声音数据,我们需要读取声音文件并进行预处理,如去除噪音、将声音信号分帧等。然后,通过特定的算法如梅尔频率倒谱系数(MFCC),来提取声音的关键特征(图5-17)。MFCC能够捕捉声音的音调、音色等重要信息,并将其转换为向量形式,以便后续的分析和处理。
接下来,让我们通过几个实例来感受一下不同声音信号的波形图(图5-18)。首先是人声的波形图,我们可以观察到人声在频谱上有明显的共振峰,这反映了声音中的特定频率成分和音色。接着是音乐的波形图,音乐的声音信号通常更加复杂,频谱上展现出多种频率成分和谐波,这反映了不同乐器和声音元素的结合。然后是环境声音的波形图,例如风声、雨声等,它们的频谱通常比较宽广,涵盖了较广泛的频率范围。这种宽泛的频谱反映了环境声音中多样化的声音元素和声音源。通过分析这些声音信号的波形图,我们能够深入理解不同声音的特性和结构。这种分析不仅帮助我们识别和理解声音内容,还能够指导声音处理和应用领域的技术优化和创新。
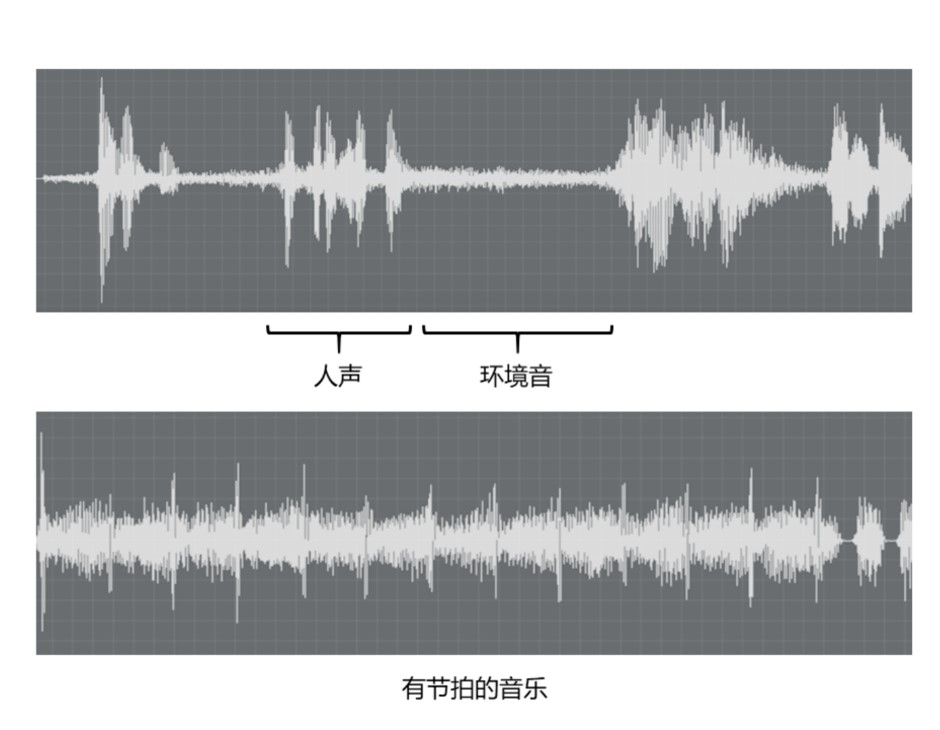
我们直观地了解了声音信号的波形和频谱图(图5-19)。接下来请大家想象一下,这些声音数据是如何被转换为特征向量的呢?当声音信号进入我们的处理系统时,它首先被转换为波形图和频谱图,这些图像表现了声音信号在时间和频率上的变化。随后,特征提取算法介入处理,从波形图和频谱图中提取出关键特征。这些特征可能包括声音的频率分布、谱线密度、音调变化等,将它们组合成一个特征向量序列。这些特征向量成为我们分析和处理声音数据的基础。通过这些特征向量,我们能够量化声音信号的各种属性,并用于语音识别、音乐分析、环境声音检测等应用。
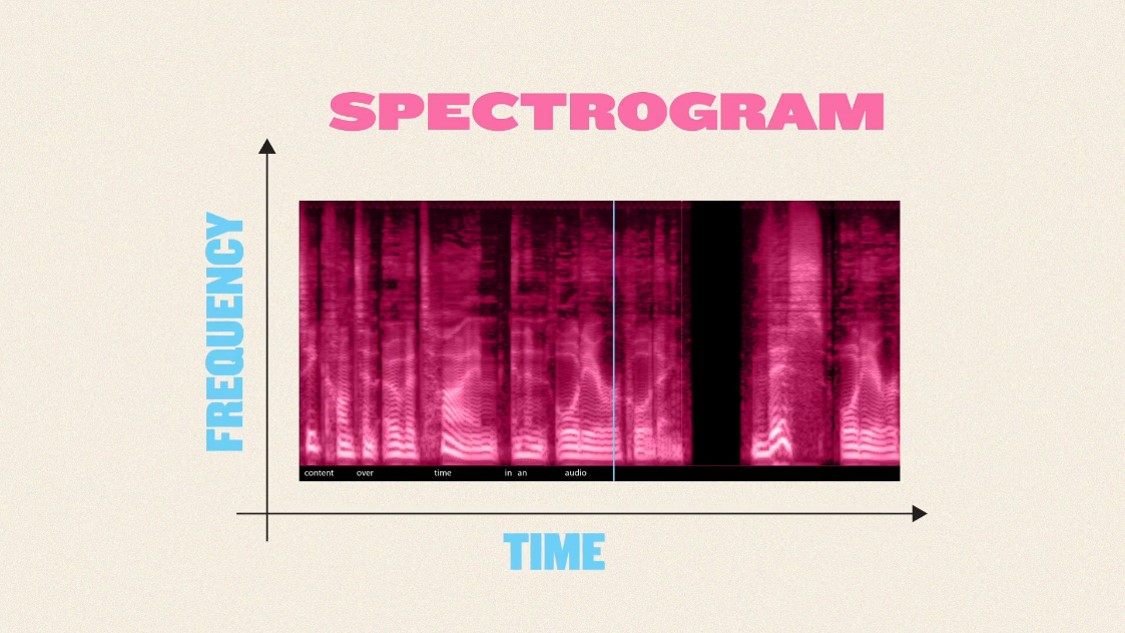
无论是词、图像、视频还是声音,它们都被转换为了可以被AI理解和处理的数据形式。这些数据形式相互交织、相互连接,构成了我们丰富多彩的数字世界。这就是数据表示的魔力。通过它,我们能够将现实世界中的信息转化为数字信号,让AI得以感知和理解。
5 矩阵乘法
为了从这些数据中提取有用信息,AI会使用各种变换方法,如矩阵乘法操作。这些变换方法能够帮助AI捕捉数据的深层特征和规律。接下来我们将深入探讨矩阵变换在数据处理和AI应用中的关键作用。
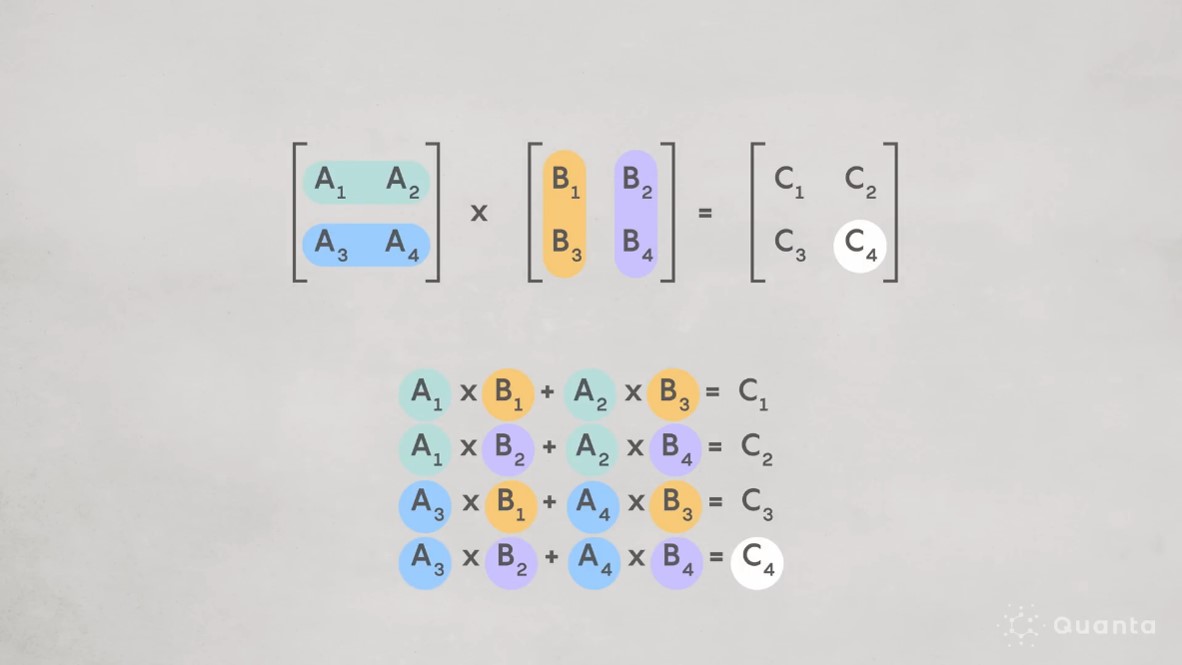
矩阵是数学中用于表示一组数的矩形阵列。如图5-20,想象一下,你有两个矩阵,A和B。A想跟B玩个“手拉手”的游戏,但有个规矩:A的列数必须和B的行数相等,这样它们才能手拉手站在一起,形成一个新的矩阵C。这个过程,就是矩阵乘法!每个新矩阵C的元素,都是A的一行和B的一列对应元素相乘后加起来的结果。这不仅仅是数字的堆砌,更是信息的融合与传递。就像是把两个世界的线索交织在一起,创造出新的故事。
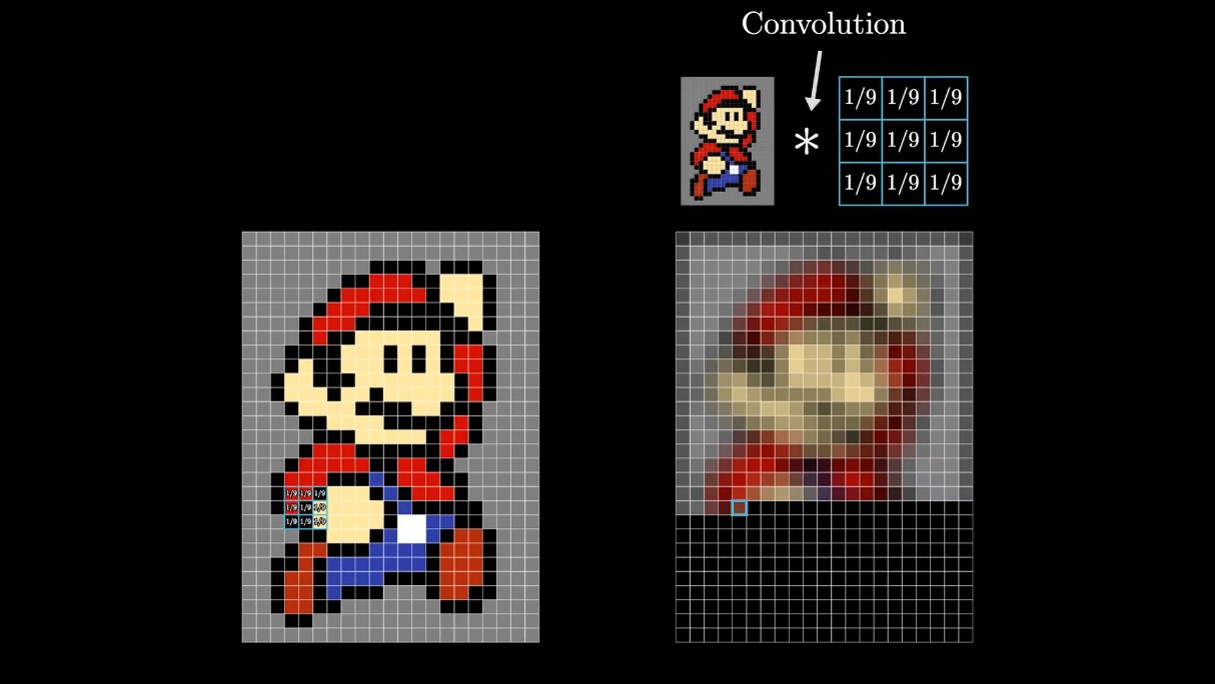
如图5-21,假设有一幅小型的图像矩阵,当你想要给这幅图像施加滤镜效果时,实际上是在对图像中的每一个像素点按照特定的滤镜规则进行变换。这些滤镜规则通常是通过矩阵乘法和卷积等数学操作来实现的。本质上,我们通过调整矩阵中的数值,对原始图像上的每一个点进行坐标变换,从而精确控制图像的变化,创造出不同的形状和视角。这种变换过程可以看作是在特征空间中重新组合和调整数据的特征,以达到我们想要的视觉效果。
在AI领域,特别是在神经网络中,矩阵乘法等表示的变换是至关重要的。矩阵乘法是计算层与层之间神经元连接的关键操作。通过矩阵乘法,可以高效地计算输入特征与权重之间的线性组合,进而实现模型的训练和推断。可以想象,神经网络就像是一个魔法师,而这些矩阵就是他的魔法棒,帮助他识别和理解世界上各种各样的事物(图5-22)。

通过矩阵乘法等数学变换,神经网络能够处理复杂的输入数据,从中提取关键特征,并作出适当的响应。这种能力使得神经网络在图像识别、语音处理、自然语言理解等领域取得了巨大的进展和应用。因此,矩阵乘法不仅仅是一种数学运算,更是推动AI技术发展的关键工具之一,为我们提供了解决复杂问题的新视角和能力。
6 总结与启发
如图5-23,AI中的数据表示形式多种多样,包括文本、图像、视频、音频等。
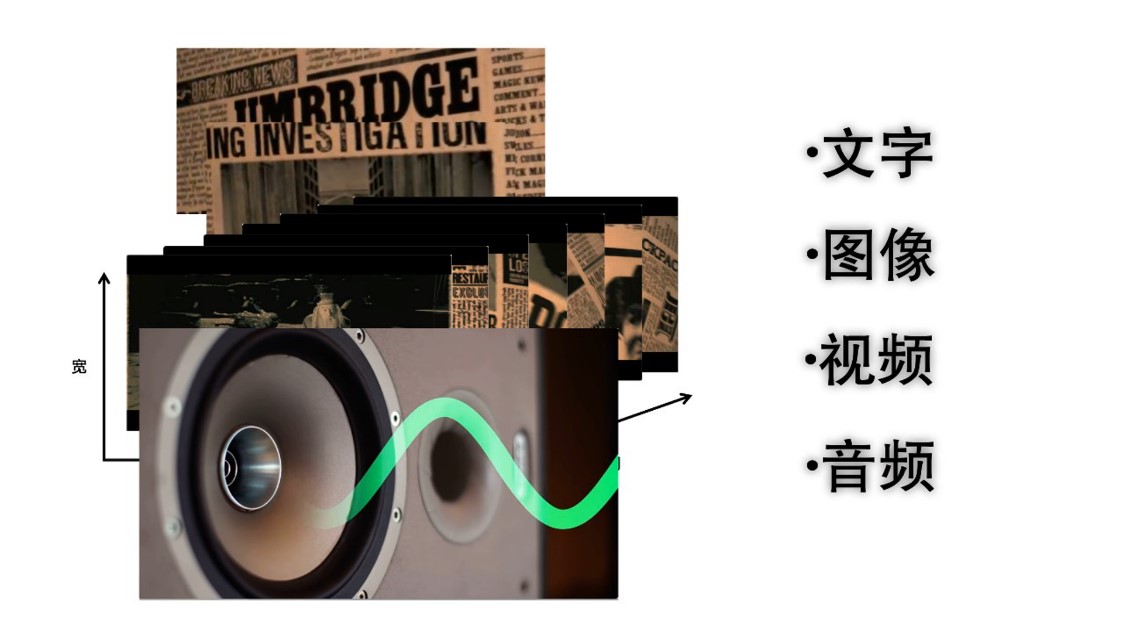
这些数据需要被转化为计算机能够理解的数学形式,如向量、矩阵、张量等(图5-24)。数据表示变换则是将这些原始数据转化为更易于模型学习和分析的形式,比如通过特征工程提取关键特征,或通过深度学习自动学习数据中的复杂模式。
在AI领域,数学基础是不可或缺的。它帮助我们理解数据背后的规律,构建有效的算法和模型。在大学学业中,同学们将会接触到《高等数学》、《数学分析》、《线性代数》、《概率论与数理统计》等课程(图5-25)。希望同学们能珍惜这些课程,打下扎实的数理基础。
